In topology, the concept of cobordism describes a seemingly simple idea: when two shapes can be seen as the boundary of a single, higher-dimensional surface, they are connected—not just spatially, but structurally. For instance, two separate circles may both sit on the edge of a cylinder. The circles are 1-dimensional, the cylinder is 2-dimensional, and the relation between them is not merely visual or geometric—it is topological. They are part of a shared continuity that exists in a space they themselves cannot occupy.
This idea, precise and formal in mathematics, becomes something far more profound when abstracted to general systems. Cobordism provides a way to rethink how all systems—not just geometric objects, but observers, models, languages, and even realities—are held in relation to one another.
At the heart of this is a simple inversion: the most important thing about a system is not what it contains, but how it differs. And that structured difference, when recursively entangled, does not just exist between systems. It is the space in which they appear at all.

What Cobordism Is—Clearly
Let’s define it cleanly.
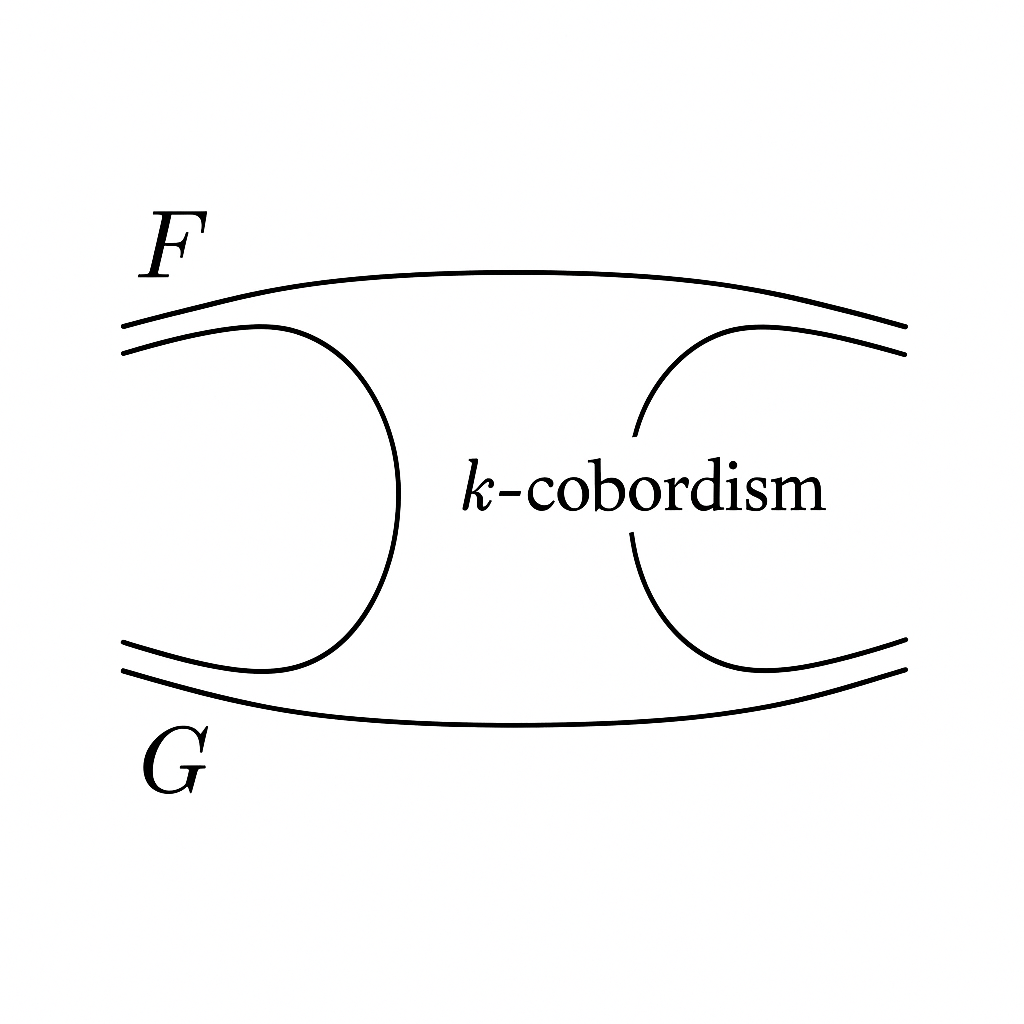
Cobordism says that two objects—specifically, two closed N-dimensional manifolds—are cobordant if they form the boundary of a -dimensional manifold. This N-manifold is the cobordism itself. The key insight: the cobordism is not a third object beside them, but a higher-dimensional relation that exists only because the two boundaries themselves do.
It’s a kind of abstract bridge. But not like a structure spanning two islands—more like a field whose very surface folds the islands into the same system.
The idea generalizes. Any two systems—biological, computational, linguistic, ontological—may be understood as distinct “frames,” whose misalignment generates a shared structure that neither fully contains, nor can fully describe. This structure is the cobordism. It is between the systems, but not of them.
And crucially, to either system, the cobordism appears invisible. Or rather, it appears as unresolved tension, as paradox, as complexity. From inside the system, the cobordism looks like infinity—a structure that cannot be completed, closed, or absorbed.

Difference Is Not a Flaw
Most frameworks for understanding the world begin with things. Entities, components, agents—each definable, bounded, classifiable. We then describe how these things interact: causally, spatially, linguistically. But what if this is backwards?
Cobordism suggests that the continuity we associate with space and time is not what precedes systems, but what emerges between them. Space is not a background container. It is the smoothing of structural difference into a usable medium.
So when two systems do not align—when there is drift between models, contradiction between perspectives, recursive incompatibility between frames—we shouldn’t interpret that as failure. We should recognize it as the precondition for any continuity at all.
This structured difference is not the residue of failed symmetry. It is the field in which systems emerge, act, and propagate. It generates the very fabric we interpret as coherence.

The Orbit Frame: Misalignment as Structure
Imagine two systems: F and G. They are not identical. They cannot be. Their observations, actions, or reference frames are distinct. Yet they interact. The pattern of that interaction cannot be flattened. It loops back on itself. It generates logical torsion—not in the geometric sense of twist in space, but in the topological sense of curvature in relation.
This is the orbit frame: a dynamic relational structure that never stabilizes into unity. What it stabilizes into instead is a kind of spinning field—driven by irreducible difference. The field that forms between and is the Δ-Field—a phase space defined not by presence, but by structured misalignment.
And that Δ-Field is not passive. It propagates. It accumulates. It twists into further structure. The orbit isn’t a trajectory in space—it is the logical field curvature that cobordism sustains.
Space Emerges from Relation
If space appears continuous, it is not because it is. It is because systems maintain coherence across difference. That coherence is cobordism made manifest at scale. In this sense, space is not what systems exist within—it is what exists when systems relate under structured tension.
Distance, from this view, is not a measure of metric separation, but of topological disparity across a shared field. Time, likewise, becomes not an axis but a rhythm—the recursive effect of local attempts to resolve irreconcilable frames.
The illusion of linearity is a function of limited perspective. The structure of reality, when seen relationally, is cobordant—not linear, but looped, entangled, curved.

Before Is No Longer Before
The hardest part of this shift is that it resists sequencing. Cobordism is not “before” systems. But it is also not “after.” It is neither cause nor effect. It is not infrastructure. It is not emergent from systems, but systems are emergent through it.
To speak of “before” here is already to have stepped outside the appropriate logic. Cobordism is non-temporal. It generates temporal effects—loops, spirals, cycles—but it is not itself within time. Nor is it a thing in space. It produces space. It is the topological differential from which dimension and distinction arise.
The Final Frame
Cobordism isn’t just a way of connecting systems. It’s the precondition for connection. Not in a metaphysical sense, but in the exact, formal sense that structured difference is necessary for any topology, any information, any coherence to exist.
It explains why systems can never fully coincide. Why every observation is partial. Why meaning must drift. Why continuity requires curvature. And why the “between” is never empty.
In a world of systems, models, and observations, cobordism is the hidden manifold—folded into every relation, saturating every interaction, silently giving rise to what we think of as structure.
We never see it directly. But we see through it.
And its torsion is what keeps the system spinning.
