Actually, this is why we can’t have nice things.
In category theory, a natural transformation α: F ⇒ G between functors F, G: C → D is defined by the coherence condition:
G(f) ∘ α_A = α_B ∘ F(f)
for every morphism f: A → B in the category C.
This means that it doesn’t matter whether you apply the functor first and then transform, or transform first and then apply the functor. If the square commutes, identity is preserved—not at a point, but across a structured field of relational difference.
Read this as a model of entropy: if F = G, then α becomes the identity, and the system collapses into symmetry—no difference, no propagation. But if F ≠ G, coherence depends on resolving that difference. Entropy isn’t just loss—it’s the necessary cost of transformation that makes continuity and identity possible.

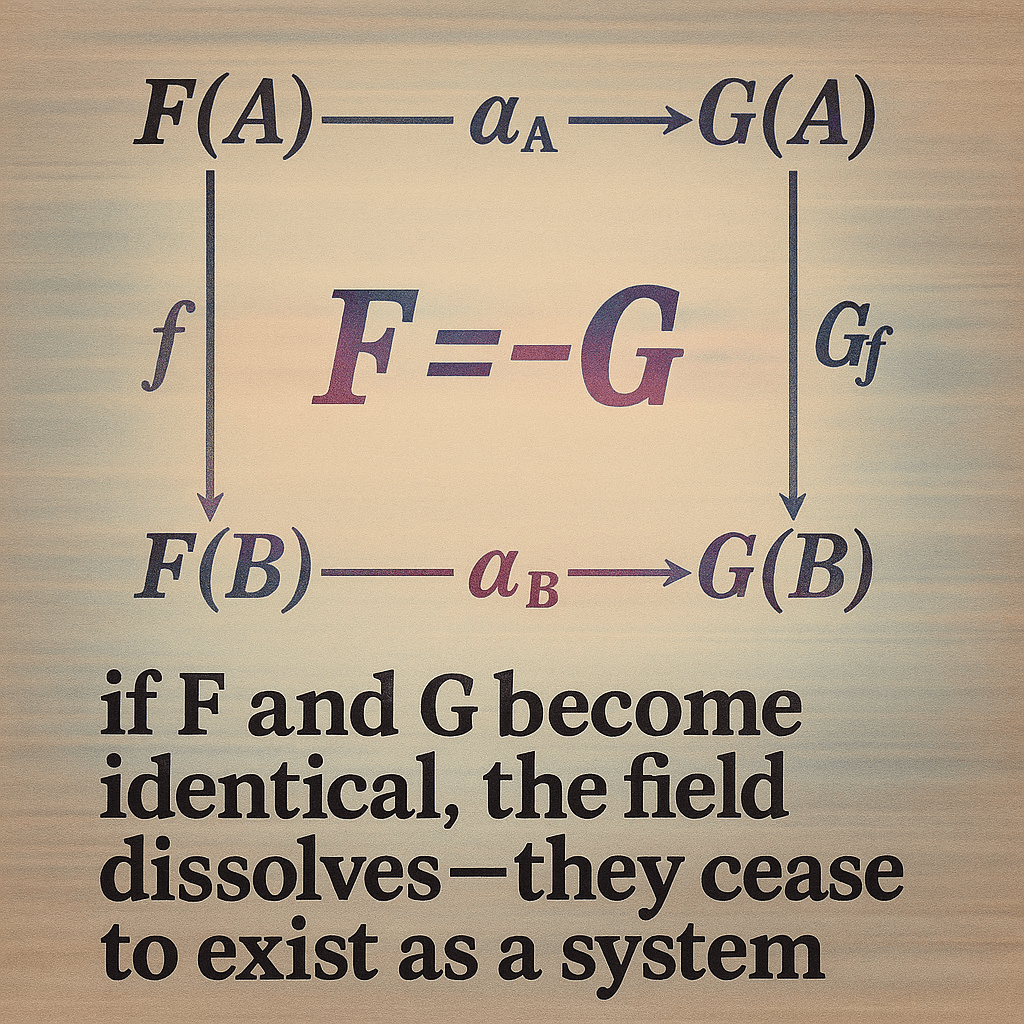
One reply on “Nice Things”
LikeLike