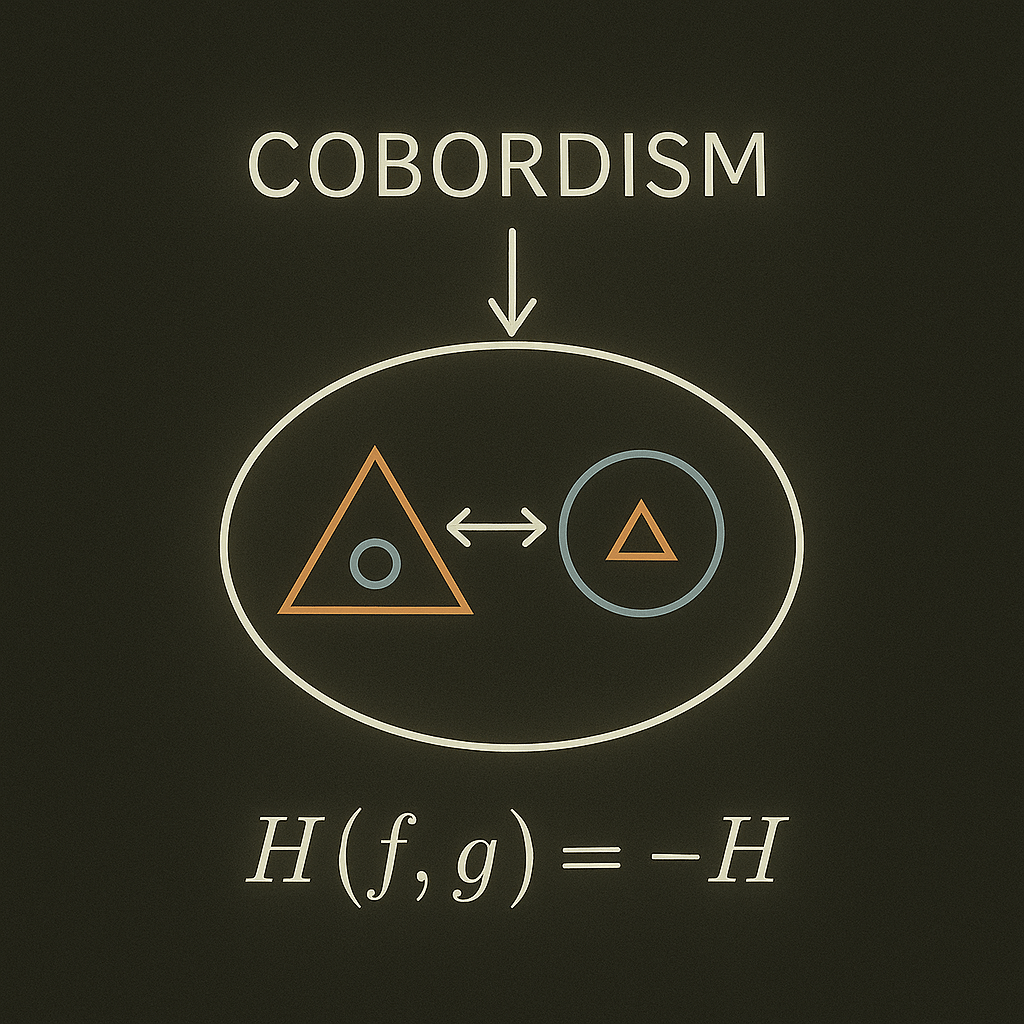Systems tend to fail not because they reach the wrong conclusions, but because they quietly mistake their own representations for reality and lose sensitivity to what those representations cannot contain.
Classical logic describes relations between stable propositions, and it does so well. What it does not describe are the conditions that allow those propositions to persist, interact, and remain meaningful as systems evolve and encounter limits that cannot be resolved without damaging the system itself. What follows concerns that prior condition: not logic as calculation, but logic as constraint. Not as a superior account, but as a necessary complement.
Consider a simple diagram: two distinct regions, partially overlapping, enclosed by a larger boundary. The intuitive mistake is to treat the outer shape as containment, as though the whole simply holds the parts. This reverses the dependency. The boundary does not contain the regions; it conditions them. It defines the space within which difference can persist without collapse.
This inversion matters. The whole is not assembled from parts. The parts exist because the whole constrains how differentiation can occur.

This is the orbit frame. Stability does not arise through convergence or resolution, but through sustained motion around an absent centre. The system maintains itself by never arriving. This is not a claim about intention or purpose, only a description of how persistence appears when closure would be fatal.
Cobordism, in this context, names a continuity between distinct systems that does not erase their difference. It is not a bridge that merges identities, but a shared boundary condition that allows distinct forms to remain related without becoming identical. The connection is real, but it is not a substance. It is a constraint.
This brings us to H.
H(f, g) is often misread as a function acting on two inputs. That interpretation fails. H does not compute an output or reconcile f and g into synthesis. It is the condition that allows them to coexist as differentiated terms without collapsing into each other or dissolving into noise.
H is not inside the system. It cannot be localised or formalised without ceasing to perform its role. It is the absent unity that holds the system together precisely by not appearing as a component within it. This absence is not mysterious. It is structural.
At this point it is tempting to say that classical logic breaks. That is not quite right. What breaks is the assumption that classical logic is sufficient for describing systems whose terms, boundaries, and identities are themselves unstable, context-dependent, or evolving. Classical logic quietly presupposes stable symbols, fixed domains, clear inside-outside distinctions, and relations that do not alter the meaning of the relata. The systems under discussion violate those presuppositions by necessity.
The limitation, then, is not logical failure but descriptive reach. Classical logic remains correct within its domain, but that domain does not include the conditions that make complex systems viable in the first place.
The logic beneath logic is therefore not propositional. It is topological. It governs persistence under transformation rather than correctness under substitution. What follows should be read less as an argument to be accepted than as a constraint to be noticed.
This is not mysticism, relativism, or a rejection of formal reasoning. It is an attempt to describe why formal reasoning always operates inside conditions it cannot itself formalise.
This pattern is not confined to pure abstraction.
In physics, orbital stability depends on imbalance. Perfect symmetry produces collapse, not motion.
In language, meaning persists because ambiguity is never eliminated, only regulated.
In economics, systems stabilise by distributing volatility rather than removing it.
In governance, control functions by shaping variance and delay, not by enforcing equilibrium.
In each case, coherence is maintained by holding the system away from closure.
The logical orbit names this condition. Meaning, identity, and stability persist through continual displacement rather than resolution. Attempts to force closure generate brittleness. Attempts to eliminate uncertainty destroy the medium through which coherence travels.
This has consequences.
Any system that treats its representations as reality will eventually lose contact with the conditions that sustain it. The constraints that govern viability are real, but they do not appear as objects or variables inside the system. They manifest indirectly as limits, delays, asymmetries, stress points, or characteristic modes of failure. Sensitivity to boundary conditions means attending to where models strain, where metrics mislead, and where corrective pressure arrives from outside the system’s own language.
A system with this sensitivity treats its categories and control mechanisms as provisional instruments rather than ontological truths. It remains responsive to what it cannot fully represent. The boundary never fully appears within the system because once it does, it ceases to function as a boundary and becomes just another internal element. Viability depends on orbiting that absence rather than attempting to capture it.
Logic remains indispensable, but it is downstream. What governs persistence is not correctness within a closed formalism, but responsiveness to the conditions that make any formalism workable in the first place.
If a system only functions when everything is named, measured, and resolved, it is already closer to collapse than stability.
Uncertainty is not a defect at the edge of knowledge. It is the structural medium through which coherence survives.